Pseudo Réciproque TAF
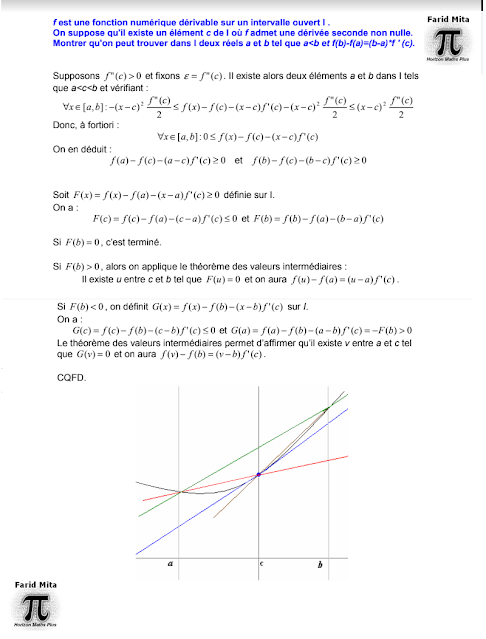
f est une fonction numérique dérivable sur un intervalle ouvert I . On suppose qu'il existe un élément c de I où f admet une dérivée seconde non nulle. Montrer qu'on peut trouver dans I deux réels a et b distincts tels que f(b)-f(a)=(b-a).f ' (c) Télécharger une solution