Dans quels cas l'écart-type est-il égal à l'écart moyen?

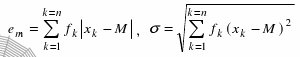
Le but de cet exercice est de caractériser les séries statistiques réelles dont l’écart moyen et l’écart-type sont égaux.

Un résultat très intéresssant:

L'écart moyen est toujours inférieur à l'écart-type.

Le seul cas (non trivial) où ces deux écarts sont égaux est lorsque la série statistique est composée de deux "mesures" de même fréquence.

On a essayé de répondre le plus simplement possible aux questions posées, sans vouloir utiliser l'inégalité de Cauchy-Shwarz.

Voir l'énoncé et la solution de l'exercice sous format PDF.

Dans le cas où vous rencontrez un problème d'affichage ou de téléchargement, réessayez avec ce lien.

Suites récurrentes d'entiers dont le "démon" de Syracuse

Voici un exercice sur les suites récurrentes que vous ne risquez pas d'avoir en colle ou dans une épreuve écrite de mathématiques!

Question 1:

En principe, répondre à cette question ne doit pas poser de grandes difficultés.

Avant de vouloir conjecturer, examiner d'abord cette autre situation (Syracuse légèrement modifiée): 

Question 2: 

Mise-en-garde pour les non-avertis: les plus brillants des grands mathématiciens se sont cassés les dents en voulant résoudre la "Conjecture de Syracuse"!

Voici un autre énoncé, mais inédit, sur lequel vous ne pouvez pour le moment que conjecturer : 

Question 3: 

Et ne voulant pas vous laisser partir sans rien "remporter" avec vous tout en vous remerciant pour cette visite au blog, je vous propose ce petit énoncé bien amusant:

Question 4:

Est-il suffisant de supposer l'application  f strictement croissante pour pouvoir l'exprimer explicitement ?

Comme l'a dit mon ami MathOMan sur son blog: "Même des questions connues et d'apparence très simple nous surprennent encore"...

NB: Le contenu de ce message est en perpetuel changement. Certains commentaires formulés par les lecteurs de ce blog, y seront insérés, partiellement ou intégralement sans préavis...