Suites récurrentes d'entiers dont le "démon" de Syracuse
Voici un exercice sur les suites récurrentes que vous ne risquez pas d'avoir en colle ou dans une épreuve écrite de mathématiques!
Question 1:

En principe, répondre à cette question ne doit pas poser de grandes difficultés.
Avant de vouloir conjecturer, examiner d'abord cette autre situation (Syracuse légèrement modifiée):
Question 2:

Mise-en-garde pour les non-avertis: les plus brillants des grands mathématiciens se sont cassés les dents en voulant résoudre la "Conjecture de Syracuse"!
Voici un autre énoncé, mais inédit, sur lequel vous ne pouvez pour le moment que conjecturer :
Question 3:

Et ne voulant pas vous laisser partir sans rien "remporter" avec vous tout en vous remerciant pour cette visite au blog, je vous propose ce petit énoncé bien amusant:
Question 4:
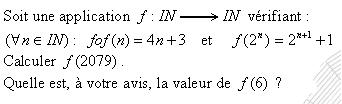
Est-il suffisant de supposer l'application f strictement croissante pour pouvoir l'exprimer explicitement ?
Comme l'a dit mon ami MathOMan sur son blog: "Même des questions connues et d'apparence très simple nous surprennent encore"...
NB: Le contenu de ce message est en perpetuel changement. Certains commentaires formulés par les lecteurs de ce blog, y seront insérés, partiellement ou intégralement sans préavis...
 |
| Cliquer sur l'image pour télécharger une autre étude sur des suites ultimement cycliques |
Je me permets de répondre à la 1ère question:
RépondreSupprimerD'abord, je remarque que tous les termes de la suite sont des entiers et sont même tous non nuls.
Ensuite, il est facile de voir que la suite est décroissante et minorée donc convergente.
Et comme les termes sont des entiers, la suite est alors constante à partir d'un certain rang, donc stationnaire.
Sa valeur constante c est impaire (sinon on aurait c=c/2 donc c=0 !!) et par suite c=(c+1)/2 c'est-à-dire c=1.
Pour la seconde question, on ne peut pas dire que la suite est monotone!
Mais, j'ai fait le calcul pour N allant de 1 à 3000 et j'ai obtenu toujours une suite stationnaire!
Je pourrai conclure que cette suite est toujours stationnaire pour toute valeur d'initailisation N.
Reste la preuve!! Je sens que je vais y arriver!
Donc, à très bientôt!
J'ai vérifié pour N allant de 3001 à 10000, et la suite est toujours stationnaire.
RépondreSupprimerCependant, je n'arrive toujours pas à "dompter" la deuxième suite!!
Pour u_n>=2, la première suite est strictement croissante. Si on ajoute le fait qu'elle est toujours plus grande que 1, et que 1 est un point fixe, on conclut.
RépondreSupprimerPar contre, le deuxième problème est connu sous le nom de "conjecture de Syracuse", et l'état des mathématiques actuelles ne peut pas statuer sur la question. On peut seulement donner une preuve heuristique : quand u_n est pair, f(un) est multiplié par 1/2, et quand un est impair, il est multiplié par (environ) 3/2. Si on tombe en moyenne autant de fois sur des entiers pairs et sur des entiers impairs, on multipliera en moyenne u_n par 3/4<1. Et donc, la suite converge presque surement vers 1...
Alors, ça ce n'est pas du "fair play" de poser des problèmes dont on ne connaît pas de solution (et personne d'autre non-plus). Depuis une semaine j'y pense et j'ai perdu environ une journée avec ça...
RépondreSupprimerCe commentaire a été supprimé par un administrateur du blog.
RépondreSupprimerA MathOMan:
RépondreSupprimerAlors là, vous me surprenez! Vous dites que vous ne connaissiez pas la Conjecture de Syracuse, et que vous croyez que vous avez perdu toute une journée à y travailler!
Je ne crois pas que vous avez effectivement travaillé pour rien! Au moins, vous vous êtes appliqué et avez mobilisé toutes vos compétences mathématiques, cognitives et savoir-faire, pour essayer de formuler déjà certaines hypothèses, voire mêmes d'autres propositions équivalentes, après avoir manipulé quelques nombres choisis comme valeurs d'initialisation. Mais, à la fin, vous avez senti, comme nous tous d'ailleurs, que la suite était "indomptable".
Cependant, en revenant sur la littérature autour de cette conjecture, vous pourriez comparer vos réflexions, hypothèses, résultats avec ceux déjà exprimés par nos prédécesseurs dans la recherche mathématique. Ce qui représente pour moi, pour nous, un très grand exploit! En ce sens que si nous nous étions intéressés à cette conjecture, depuis sa première formulation, nous aurions trouvé la même chose que ceux qui l'ont déjà fait! En d'autres termes, la méthodologie de la recherche est la même, que ça soit dans les années 60 ou de nos jours. Pour être clair, je cite l'exemple d'un étudiant, disons un apprenti-mathématicien qui essaie de résoudre un problème classique pour la première fois, de ses propres moyens et qu'il réussit à le faire de la même manière, sinon plus meilleure que celle déjà connue dans les manuels de mathématiques. N'est-ce pas là un exploit?
Pour la mise-en-garde, c'était programmée!
En effet, j'ai reçu une vingtaine de réponses, généralement fausses que je n'avais pas voulu mettre en ligne! Sur ce, j'ai jugé opportun d'indiquer les références sur la dite conjecture étant donné que je viens de découvrir que certains ignoraient toujours l'existence d'un groupe de conjectures non sans preuve, mais indécidables.
Quand avais-je pensé à proposer cette conjecture?
C'est à la suite de l'annonce du refus de Grigori Perelman de recevoir son prix pour ses remarquables travaux dans la recherche mathématique notamment sa preuve de la Conjecture de Poincaré...
Je me permets d'ajouter dans cette réponse que je suis toujours entrain de penser à cette conjecture de Syracuse, et que j'y travaille toujours, en faisant recours à tous les outils mathématiques dont on dispose actuellement. J'ai pu formuler d'autres conjectures équivalentes que je pense plus "faciles" à manipuler dont celles utilisant la notion de valeur d'adhérence, ou encore les polynômes générés à partir de la représention binaire des entiers naturels...
Voilà, je n'en dirai pas plus! Car, je trébuche toujours!!
;)
Oui, en fait je connaissais pas du tout cette conjecture. En plus, il y a quelques semaines vous aviez dit dans un commentaire (supprimé entre-temps) qu'on pouvait résoudre le problème avec une récurrence astucieuse. C'était donc dans cette voie que j'ai cherché...
RépondreSupprimerEl Jj dit :
"quand u_n est pair, f(un) est multiplié par 1/2, et quand un est impair, il est multiplié par (environ) 3/2. Si on tombe en moyenne autant de fois sur des entiers pairs et sur des entiers impairs, on multipliera en moyenne u_n par 3/4<1."
Ce n'est pas si évident car la moyenne entre 1/2 et 3/2 est 1 et pas 3/4.
Effectivement, j'ai commenté sans me relire (deux coquilles en 11 lignes, j'améliore pas ma moyenne) : en moyenne, on multiplie par 3/4 tous les deux pas (et donc par sqrt(3)/2 par pas). Effectivement, c'est de l'information Wikipédia, mais je n'ai jamais prétendu que c'était quelque chose de personnel !
RépondreSupprimerCela dit, j'étais tombé il y a quelques temps (le 27 mai 2007, pour être précis : http://eljjdx.canalblog.com/archives/2007/05/27/5092712.html) sur un article de CyberScience qui parlait de la démonstration probabiliste de la conjecture qui statuait sur le fait que les suites de syracuse convergent "presque surement" vers 1. Une démo probabiliste, donc.
En tout cas, je te souhaite bon courage pour tenter d'avancer dans la démonstration, même si j'ai tendance à penser qu'on ne s'en sortira pas si facilement, surtout que le problème généralisé est indécidable.
Réponse à El Jj:
RépondreSupprimerIl me semble que tu as mal interprété un certain passage dans mon dernier commentaire!
En fait, je voulais dire que la preuve heuristique a été reproduite par beaucoup de gens depuis les années 60 pour te déculpabiliser devant MathOMan qui a décelé une erreur (?!!) dans ton raisonnement.
Pour l'occasion, je tiens à signaler que je n'ai pas encore terminé ma réponse au dernier commentaire de MathOMan, surtout la partie relative aux preuves heuristiques de cette fameuse conjecture...
J'ai beau cherché la démonstration probabiliste sur le web, mais en vain! De toute façon, je ne crois pas qu'elle permet de prouver la conjecture!! Mes raisons? Dans un prochain billet...
Bjr,
RépondreSupprimerJe suis l'un de vos anciens étudiants.
J'essaie de répondre à l'exercice 4:
En utilisant les deux propriétés de f, j'essaie de remonter vers une puissance de 2. Ainsi:
f(2079)=fofof(519)=fofofofof(129)=fofofofofof(64)=fofofof(259)=fof(1039)=4159
Résultat: f(2079)=4159
Déjà, on pourrait voir que:
f(1)=3, f(2)=5, f(3)=f(f(1))=7, f(4)=9, f(5)=f(f(2))=11, f(7)=f(f(3))=15, ...
mais f(6)=? et même f(0)=?
ça a l'air de prendre f(n)=2n+1
En tout cas, la récurrence ne peut s'appliquer!
Si, en plus, je suppose que f est injective, alors f(f(0))=3=f(1)
donc f(0)=1
C'est le cas de f strictement croissante.
Je dois d'abord réfléchir...
Pour la 3, on peut montrer facilement que la suite est bornée et donc ultimement périodique.
RépondreSupprimerCependant, j'ai vérifié sur un ensemble de valeurs de N que la suite est stationnaire de valeur constante nulle.
Voilà! Je crois que cette suite est aussi difficile que celle de Syracuse...