.:Horizon Maths Plus:.

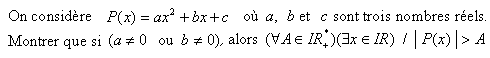
Parfois, il serait plus facile de montrer que la proposition contraposée est vraie, à condition de bien formuler les négations des propositions, surtout si elles sont quantifiées (universel et existentiel) Voici un exemple :  Cliquer sur l'image pour afficher le texte en arabe    Mais, la résolution de  l'exercice est très difficile à mener par des élèves de lycée, les nouveaux apprenti-mathématiciens! Pourtant, on le trouve dans le manuel officiel de SM1 du programme marocain! L'énoncé proposé dans ce même manuel est tout autre. Il comporte une erreur! Comme d'ailleurs, un grand nombre d'exercices qui s'y trouvent!! C'est désolant... Corrigé:

Un exemple d'une égalité à démontrer par récurrence. Chaque fois que l’égalité est précisée dans l'énoncé, on pourra raisonner par récurrence. Comme c'est le cas ici! Cliquer sur l'image pour afficher le texte en arabe Parfois, même si l’égalité n’est pas donnée, on commencera par calculer les premiers termes pour essayer de voir quelle serait l’expression du terme du deuxième membre en fonction de n, dans le cas général. Et c’est le raisonnement par récurrence qui permettra de ‘‘valider’’ cette expression formulée !   Cliquer sur l'image pour afficher le texte en arabe    Attention, ce même exercice peut être résolu différemment! Par décomposition en éléments simples... Question de temps!

Le trio 123 est un collier Est-il possible de partager un ensemble de 15 billes bicolores en deux parties de telle manière à ce qu'il n' y est aucun  collier dans chacune des deux parties? On appelle  collier , un ensemble formé par autant de billes que de couleurs. On précise qu'on a une seule bille pour chaque paire de couleurs choisies parmi 6 et donc jamais une paire ne peut constituer un  collier .

Tout point du plan affine est coloré par une et une seule couleur. Dans le cas où  toutes les droites du plan sont unicolores ou bien bicolores, quel est le nombre maximum de couleurs pouvant être utilisées?

  Cliquer sur les images pour afficher le texte en Arabe 

Un exemple de raisonnement par l'absurde:  Cliquer sur l'image pour afficher le texte en Arabe       . . .

Un exemple d'inégalité à démontrer par récurrence. L'énoncé et la réponse sont en image, en français et en arabe. Pour les avertis, on pourra utiliser le binôme de Newton pour établir la même inégalité, sinon étudier le signe d'une fonction numérique d'une variable réelle en partant de la différence entre les deux membres de l'inégalité (étude des variations) NB: Cette inégalité porte le nom de Bernoulli.

La théorie des situations didactiques Cours donné lors de l’attribution à Guy Brousseau du titre de Docteur Honoris Causa de l’Université de Montréal Définition: Une situation est l’ensemble des circonstances dans lesquelles une personne se trouve, et des relations qui l’unissent à son milieu. Prendre comme objet d’études les circonstances qui président à la diffusion et à l’acquisition des connaissances conduit donc à s’intéresser aux situations. Les situations didactiques sont, dans la langue française, des situations qui servent à enseigner. Deux points de vue s’opposent alors : Selon le premier, la situation est l’environnement de l’élève mis en oeuvre et manipulé par l’enseignant ou l’éducateur qui la considère comme un outil. Selon le second, la situation didactique est l’environnement tout entier de l’élève, l’enseignant et le système éducatif lui même y compris. Par Guy Brousseau Pr. Emérite (IUFM d’Aquitaine) Lire ou télécharger le document La théorie des situations didactique...

Obstacles épistémologiques, conflits socio-cognitifs et ingénierie didactique 1989 Ce texte se compose de deux parties: - Dans la première je propose de distinguer un certain nombre de concepts : obstacle épistémologique, obstacle cognitif, et d’envisager le rôle des conflits socio-cognitifs dans leur évolution - La deuxième est un essai de terminologie. J’y étudie les relations qu’entretiennent à priori, dans le cadre de la didactique, les conflits socio-cognitifs et les obstacles épistémologiques. Par Guy Brousseau Université de Bordeaux I Titre du texte: Obstacles épistémologiques, conflits socio-cognitifs et ingénierie didactique Langue Français Date de production, écriture 1989 Equipe de recherche IREM de Bordeaux Nom de la revue ou de l’ouvrage : Construction des savoirs , Obstacles et Conflits Sous la direction de Nadine Bednarz, Catherine Garnier Editeurs: CIRADE Les éditions Agence d’Arc inc. Date de publication 1989 Page 277-285 Mots-Clés: Obstacles épistémologiques, mathémat...

Les obstacles épistémologiques et la didactique des mathématiques 1989 L’auteur s’est intéressé à la notion d’obstacle épistémologique après avoir observé les avantages du saut de complexité. L’introduction d’un aspect nouveau de certaines notions déjà apprises (par exemple l’enseignement de divisions dans les décimaux après celle des divisions euclidiennes) est plus facile si les situations nouvelles sont très différentes – plus complexes – que si elles le sont peu. L’ancienne conception persiste et provoque des erreurs dans l’usage de la nouvelle. L’évolution ordinaire, par hérédité directe et petites modifications, créée des difficultés d’apprentissage spécifiques.Ce fait fut rapproché de la notion d’obstacle épistémologique dans l’histoire des Sciences expérimentales. L’article donne un résumé des résultat de quelques unes des recherches effectuées entre 1975 et 1988 qui ont montré l’existence d’obstacles épistémologiques en mathématiques, soit par des expériences d’enseignement qu...