Raisonner par contraposée (proposition quantifiée)

Par Farid Mita -
Parfois, il serait plus facile de montrer que la proposition contraposée est vraie, à condition de bien formuler les négations des propositions, surtout si elles sont quantifiées (universel et existentiel)

Voici un exemple :

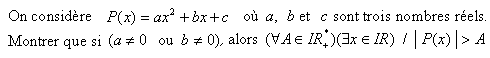Cliquer sur l'image pour afficher le texte en arabe
  Mais, la résolution de  l'exercice est très difficile à mener par des élèves de lycée, les nouveaux apprenti-mathématiciens! Pourtant, on le trouve dans le manuel officiel de SM1 du programme marocain! L'énoncé proposé dans ce même manuel est tout autre. Il comporte une erreur! Comme d'ailleurs, un grand nombre d'exercices qui s'y trouvent!! C'est désolant...

Corrigé:

Commentaires

  1. Anonymous9 octobre 2010 à 19:49

    c'est troooooop difficile

    RépondreSupprimer
  2. Farid Mita9 octobre 2010 à 22:19

    Effectivement, c'est très difficile pour le lycéen!!!
    Pour le supérieur, il suffit d'appliquer un résultat concerant les fonctions polynômes à coefficients réels ( les seules qui soient bornées sur IR sont les fonctions constantes) sinon par passage à la limite.
    Pour le lycéen, il faut impérativement détailler les questions en lui proposant la méthode à suivre, sans oublier de lui demander de montrer d'abord que le seul réel positif qui soit inférieur à tous les réels strictement positifs est le réel nul.

    Je rappelle que j'avais bien dit dans le post que la résolution de l'exercice était très difficile à mener par des élèves de lycée!!

    RépondreSupprimer

Enregistrer un commentaire

Merci de laisser un commentaire!