Collier de billes bicolores
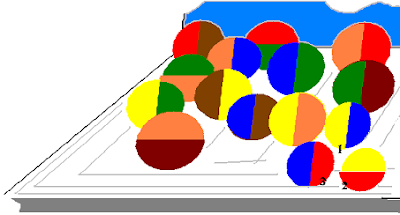 |
| Le trio 123 est un collier |
Est-il possible de partager un ensemble de 15 billes bicolores en deux parties de telle manière à ce qu'il n' y est aucun collier dans chacune des deux parties?
On appelle collier, un ensemble formé par autant de billes que de couleurs.
On précise qu'on a une seule bille pour chaque paire de couleurs choisies parmi 6 et donc jamais une paire ne peut constituer un collier.
La réponse est Non
RépondreSupprimerPreuve:
Considérons une partition en deux ensembles A et B.
Fixons une couleur; par exemple le Vert.
Nous remarquons qu'il y a exactement 5 billes qui utilisent le Vert.
Certaines sont dans A, d'autres dans B: 0+5, 1+4, 2+3, 3+2, 4+1 et 5+0
Bref, il y a un groupe qui contient au moins 3 billes utilisant le Vert.
Supposons que c'est A et imaginons que ces billes soient Vert-Rouge, Vert-Bleu et Vert-Jaune.
Intéressons-nous maintenant aux 3 billes Rouge-Bleu, Bleu-Jaune et Jaune-Rouge.
Ces trois billes ne doivent pas être tous dans le même B, car elles forment un collier!
Donc l'une au moins de ces trois billes est dans A.
Supposons que c'est la bille Rouge-Bleu
Les billes Rouge-Bleu, Vert-bleu et Vert-rouge forment un collier et il est dans A
Contradiction.
C'est situation n'est pas possible.
Conclusion:
Il n'est pas possible de trouver une partition en deux parties sans qu'il y au moins un collier dans l'une des parties.
Ou de manière équivalente:
Quelque soit la partition de cet e,semble de billes en 2 parties, il y a au moins une partie qui contient au moins un collier.