Gros festin pour une araignée, pauvre mouche!...
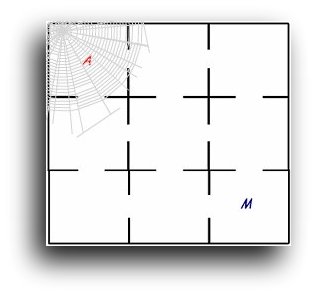
Montrer que l’araignée A finira par capturer la mouche M, en se déplaçant d’une case à l’autre, aléatoirement, même sans ses facultés naturelles ; la mouche M étant immobile dans sa case.
 |
Examiner le cas où la mouche M change aussi de cases aléatoirement, à la même vitesse constante que l’araignée A.
Voir la preuve de la première situation...
Bonsoir GRAND PROFESSEUR .Doit-on supposer que l’araignée ne retourne pas dans les cases par lesquelles elle passera ?
RépondreSupprimerOn pourra imposer cette condition, mais on tombera sur des situations de blocage; par exemple: de A vers la case de droite, puis vers la case centrale, ensuite vers la case de droite, puis vers la case du haut-droite et notre araignée ne pourra plus bouger!!
RépondreSupprimerDonc la mouche a une chance de survivre et il serait intéressant de calculer cette probabilité de rester en vie...
Donc, on permettra à la bestiole de repasser par les cases autant de fois qu'elle le souhaite, sans lui interdire de revenir à la case qu'elle vient juste de quitter.
Conseil: avant de traiter ce cas de figure 3X3, examiner celui de 2X2.
Très bonne requête!
Bonsoir. Doit on ajouter que l'araignée visitera necessairement chaque case au moins une fois ? merci.
RépondreSupprimerCe n'est pas nécessaire!
RépondreSupprimerBonsoir Monsieur .Et si l'araignée execute ,hasardement et infiniment, un aller et retour entre sa case de départ et la première case de la deusième colonne ,par exemple , attrapera -t-elle la mouche ?
RépondreSupprimerMerci Monsieur de votre patience .
Un tel événement est de probabilité NULLE, donc impossible!! (1/2*1/3*1/2*1/3*1/2*1/3......)
RépondreSupprimerVoici quelques indications pour résoudre le problème:
* On considère pour chaque case, une probabilité pour que l'araignée A s'y trouve à l'étape n.
* Grâce à la symétrie du cas de figure proposée, on aura six suites de nombres réels (compris entre 0 et 1) au lieu de neuf.
* On établit six relations de récurrence entre ces suites, en utilisant les probabilités conditionnelles.
* La suite qui nous intéresse le plus, est celle qui donne la probabilité concerant la case occupée par la mouche M.
C'est un problème classique qui se résourd normalement par la REDUCTION d'une Matrice Carrée ...
Mais il se trouve que pour notre figure, il est inutile de se lancer dans la réduction, à condition de bien examiner les équations de récurrence entre les suites pour les simplifier en une seule, mais d'ordre supérieur...
C'est faisable!
Conseil: Avant de résoudre le problème mathématiquement, on pourrait faire une simulation avec une feuille d'Excel par exemple...
Merci Monsieur .En fait , je n'ai pas bien assimilé l'énoncé du problème . Et voilà , encore , une leçon de plus que vous me donnez .Merci infiniment Grand Monsieur .
RépondreSupprimerMaintenant, vous pouvez voir la preuve, en cliquant sur le lien que je viens d'ajouter sur le post...
RépondreSupprimer